ML/AI 를 공부할 때 등장하는 확률 통계 용어를 정리하고자 합니다.
ML/AI에서 이를 다루는 이유는 확률은 불확실성을 표현하는 언어 라고 보시면 됩니다.
머신러닝, 인공지능분야는 확률의 관점에서 결론을 내리기 때문입니다.
사진학습 예시:
 [p(lion), p(tiger)] = [0.01, 0.99] |
 [p(lion), p(tiger)] = [0.98, 0.02] |
향후 관심을 가지고 현업에 계시거나 혹은, 논문을 보실 때 나올만한 용어를 정리합니다.
확률론 (probability theory) :
실제로 발생하는 다양한 결과들의 기회 혹은 가능성을 이해하거나 설명하는 이론.
표본공간과 사건 (Sample space, Event)
표본공간(sample space) : 실험에 의하여 가능한 모든 결과의 집합
사건(event) : 표본공간의 부분 집합
실험 (experiment or trial) : 확률적 기대효과를 갖는 행위
결과 (outcome) : 실험에 의하여 나타난 현상
예를 들어 6면체 주사위에서, 결과는 1 ~ 6 까지 나올수 있는 모든 경우를 뜻하고
사건이란 단일 혹은 연속적으로 주사위를 던졌을 때 일어날 수 있는 모든 사건을 뜻합니다.
개별 사건을 모두 나열한 집합을 event space라 정의하는데, 우리가 이런 용어를 배우는 이유는 확률과 사건의 집합을 표현하는 일상언어를 함축적이고 정확하게 표현하기 위함으로 알아두시면 좋을 것 같습니다.
모든 사건은 표본공간에 속한다는 아래와 같이 정의된다.

Sigma Field, Sigma Algebra:
event space를 학계에서는 sigma field라 하고 이와 관련하여 measure theory에서 sigma algebra를 배웁니다. 정의된 확률 공간에서 우리의 실험이 가져다 주는 결과는 어느정도의 확률을 가지는지를 정의하는 언어라고 이해하시면 될 것 같습니다. 이러한 부분집합과 그 확률을 정의하는 sigma algebra를 시각적으로 표현하면 아래와 같습니다.

sigma algebra에 관한 자세한 설명은 위키백과에 잘 나와 있습니다. 링크를 유첨합니다.
PDF(Probability Density Function) 와 CDF(Cumulative Distribution Function)
PDF(Probability Density Function, 확률 밀도 함수) : 연속적인 변수에 의한 확률 분포 함수를 의미합니다.
특정 확률 변수 구간의 확률이 다른 구간에 비해 상대적으로 얼마나 높은가를 나타내는 것이며, 값 자체가 확률을 의미하지 않습니다. 분포내에서 특정한 한 값에서의 확률은 0 입니다. 확률은 범위내의 pdf 영역 넓이(적분값)입니다.
P (X = p) = 0
PDF(Probability Density Function)는 두가지 특징이 있습니다.
1. 항상 양의 값을 가질 것

2) PDF 의 총 합은 1.

CDF(Cumulative Distribution Function, 누적 분포 함수) : PDF(Probability Density Function, 확률 밀도 함수)의 누적 적분확률입니다.
CDF는 누적된 확률분포 PDF는 구간 별 확률분포를 기억하시면 됩니다.
아래 그래프를 보시면 개념이해에 도움이 되실 듯 합니다.

Expectation & Variance
expectation은 기대값입니다.
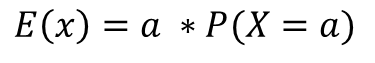
variance는 분산이고 값들이 어느정도로 흩어져 있는지 측정합니다.
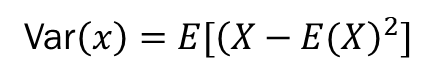
공분산 (covariance)
covariance는 공분산으로 두 개의 확률 변수의 선형관계를 나타내는 값입니다. 분산이라는 개념을 확장된 것으로, 확률 변수들의 흩어진 정도를 나타냅니다.
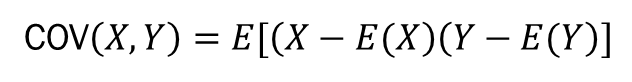
공분산 식이 위의 분산과 비슷하다는 느낌을 받을 수 있습니다. 분산식을 전개하면 아래와 같습니다. 분산의 개념을 확장해서 두 변수의 흩어진 정도임을 상기하면 충분합니다.
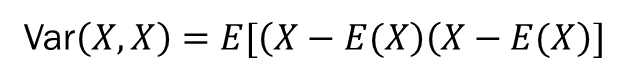
상관계수 (correlation coefficient)
공분산을 X와 Y변수의 표준편차로 나누어 -1에서 1사이의 계수를 통해서 변수간의 직선관계를 측정합니다.
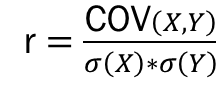
상관계수는 ML/AI에서 자주 언급되는 토픽으로 변수간의 관계를 표현하기에 효과적이기 때문입니다.
상관계수의 특징은 아래와 같습니다.
- 상관계수는 -1과 1사이에 있음.
상관계수 값의 크기는 직선관계를 나타내고, 부호는 관계의 방향임. - r > 0 - positively correlated : 한 변수의 값이 크면 다른 변수의 값도 큽니다. 직선의 기울기는 양수입니다.
r < 0 - negatively correlated : 한 변수의 값이 작으면 다른 변수의 값은 큽니다. 직선의 기울기는 음수입니다. - r = +1 : 변수의 관계는 정확한 양의 기울기 직선을 형성합니다.
r = -1 : 변수의 관계는 정확한 음의 기울기 직선을 형성합니다.
상관계수의 값이 1 또는 -1에 가까울 수록 두 변수 사이의 연관성이 크고, 0에 가까울 수록 관계가 약합니다.
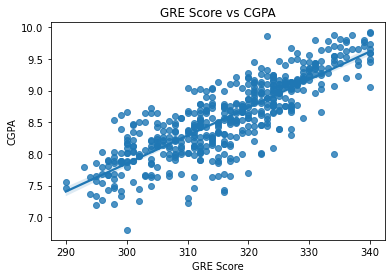
아래는 데이터로 대학원 지원자의 GRE점수와 대학학점간의 상관계수를 구해본 그래프입니다. 상관계수 0.82로 뚜렷한 양의 추세선을 보입니다.
결합확률분포(Joint Distributions)
여러변수들 간의 확률 분포를 나타낸 것입니다. 앞의 확률분포에서 변수를 늘려서 개념을 확장한 것이라 보면 됩니다.
주변확률분포 (Marginal Probability)
여러 변수로 이루어진 분포에서 특정 변수의 확률분포를 파악할 때 사용합니다. 다른 조건이 같을 때 특정 변수가 어떻게 동작하는지 파악하는데 사용합니다. 아래의 예시를 보면서 이해하면 되겠습니다.
조건부확률 (Conditional Probability)
말 그대로 특정 조건이 주어졌을 때 확률입니다. 아래 예시를 기준으로 말씀드리면
P(X=1,Y=2) = 0.03입니다. 그런데 P(X=1| Y=2) = 0.03/0.3 = 0.1 입니다. 특정 조건에서의 확률로 Markov Decision Process(MDP) 등의 분야에 나오는 핵심개념입니다.

독립 (Independence)
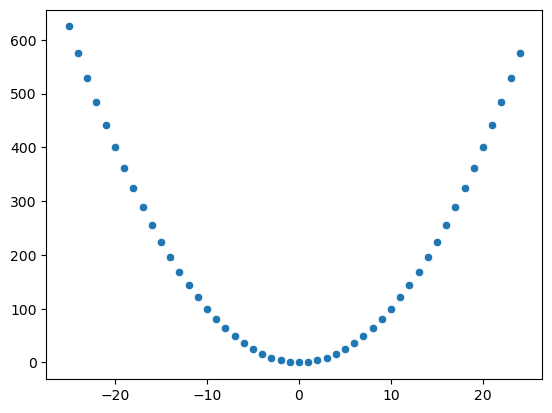
P(X,Y) = P(X) * P(Y) 로 각 변수가 다른 변수에 영향을 주지 않습니다. 한가지 주의하실 점은 독립의 경우에는 상관계수가 0이지만 상관계수가 0이라고 반드시 독립이 아니란 점입니다. 대표적인 경우는 두 변수의 관계가 직선이 아닌 경우입니다 (non-linear case)
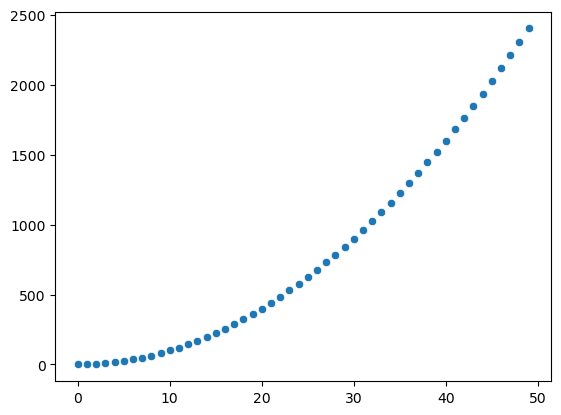
두 변수간의 관계가 분명히 존재하는데 상관계수는 직선관계만 찾으려 듭니다. 직선의 관점에서는 관계가 없기 때문에 상관계수는 0이 되는데 낮은 상관계수가 반드시 독립성을 의미하지 않게 됩니다. 명제의 역은 반드시 참은 아니다는 말 기억해 주세요. 아래 2차함수 예시를 기억하시면 더 쉽게 이해하실 수 있습니다.