선형 회귀는 통계학에서 가장 기본적인 회귀 분석 기법 중 하나로, 하나의 독립 변수와 하나의 종속 변수 간의 선형적인 관계를 모델링하는 것입니다.
선형 회귀 모델은 종속 변수(y)와 독립 변수(x) 사이의 선형 관계를 설명하기 위해 일차 함수의 형태를 사용합니다. 즉, y = mx + b 형태의 방정식으로 표현됩니다. 여기서 m은 기울기(coefficient)를 의미하고, b는 y 절편(intercept)을 나타냅니다.
선형 회귀는 다음과 같은 단계로 수행됩니다.
- 데이터 수집: 종속 변수와 독립 변수를 포함하는 데이터를 수집합니다.
- 데이터 전처리: 데이터를 정제하고 결측치를 처리합니다.
- 모델링: 선형 회귀 모델을 적용하여 종속 변수와 독립 변수 간의 관계를 모델링합니다.
- 모델 평가: 모델의 성능을 평가하고 결과를 해석합니다.
최고제곱법(Ordinary Least Squares, OLS)과 평균제곱오차(Mean Squared Error, MSE)
최소제곱법(OLS)
최소제곱법은 선형 회귀 모델에서 가중치(w)와 편향(b)을 결정하는 데 사용되는 방법 중 하나입니다. 최소제곱법은 가중치와 편향을 조정하여 예측값과 실제값 간의 제곱 오차를 최소화하는 가중치와 편향을 찾는 것입니다. 즉, 최소제곱법은 SSE (Sum of Squared Errors)를 최소화하는 가중치와 편향을 찾는 것입니다. 이 방법을 사용하면 가중치와 편향을 빠르고 쉽게 결정할 수 있습니다.
평균제곱오차(MSE)
평균제곱오차는 예측값과 실제값 간의 차이를 제곱한 것들의 평균을 계산한 값입니다. 선형 회귀 모델에서 MSE는 모델이 예측한 값과 실제 값 사이의 오차를 측정합니다. MSE는 SSE를 데이터 샘플 수로 나눈 값이기도 합니다.
(MSE = SSE / N)
최소제곱법과 평균제곱오차는 모델의 학습 및 평가에 중요한 역할을 합니다. 최소제곱법은 가중치와 편향을 결정하는 데 사용되며, 평균제곱오차는 모델의 예측 성능을 평가하는 데 사용됩니다. 따라서 이 두 가지 개념은 선형 회귀 모델을 학습하고 평가하는 데 있어서 매우 중요합니다. OLS는 위 그림의 residual error를 최소화 하기 위한 방법입니다.
회귀 분석에서 사용되는 오차 관련 지표를 소개하고자 합니다. MSE, SSE, SSR 등 회귀분석에서 오차관련 용어는 많이 들어보셨을 텐데, 각각의 개념과 오차관련 지표에 대한 관계를 이해 하시면 여기서 파생되는 ML/AI 기법과 모델에 대한 이해도를 높이실 수 있습니다.
선형회귀 설명지표들의 관계: MSE, SSE, SSR, SST
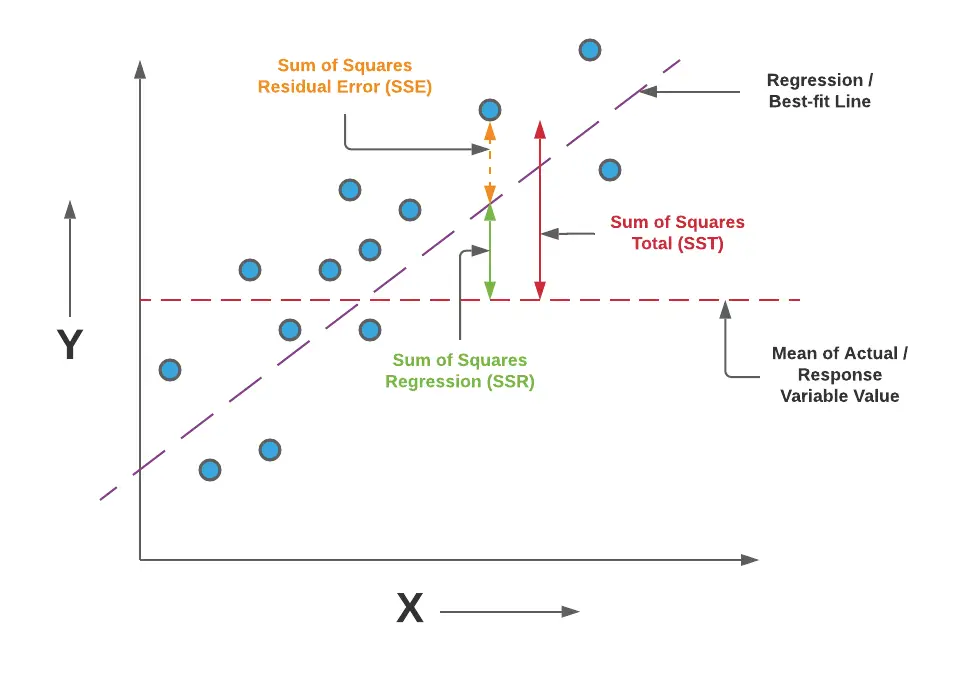
MSE (Mean Squared Error), SSE (Sum of Squared Errors), SSR (Sum of Squared Regression), SST (Total Sum of Squares)는 모두 회귀 분석에서 사용되는 오차 관련 지표입니다.
MSE (Mean Squared Error):
MSE는 선형 회귀 모델에서 예측값과 실제값의 차이를 제곱한 것들의 평균입니다. 수식으로 나타내면 다음과 같습니다.
MSE = (1/(n-k-1)) * ∑(i=1 to n) (yi - ŷi)^2 여기서 n은 샘플 데이터의 개수이고 k는 독립 변수의 개수입니다. yi는 실제값, ŷi는 모델의 예측값이고 MSE가 작을수록 모델의 예측 성능이 높다고 해석할 수 있습니다.
SSE (Sum of Squared Errors):
SSE는 모든 데이터 샘플에서 예측값과 실제값의 차이를 제곱한 것들을 모두 더한 것입니다. 수식으로 나타내면 다음과 같습니다. SSE는 회귀 모델에서 설명하지 못한 변동성(오차)을 측정하는 지표로 사용됩니다. SSE가 작을수록 모델이 데이터를 잘 설명하고 있다는 것을 의미합니다.
SSE = ∑(i=1 to n) (yi - ŷi)^2
SSR (Sum of Squared Regression):
SSR은 회귀 모델에서 설명한 변동성을 측정하는 지표로 사용됩니다. 수식으로 나타내면 다음과 같습니다. 여기서, ŷi는 모델의 예측값, ȳ는 실제값의 평균입니다. SSR은 모델이 설명한 변동성을 측정하므로, SSE와 SSR의 합은 전체 변동성(SST)과 같아집니다.
SSR = ∑(i=1 to n) (ŷi - ȳ)^2
SST (Total Sum of Squares):
SST는 모든 데이터 샘플에서 실제값과 실제값의 평균값과의 차이를 제곱한 것들을 모두 더한 것입니다. 수식으로 나타내면 다음과 같습니다. 여기서, ȳ는 실제값의 평균입니다. SST는 모델이 설명할 수 있는 변동성과 설명하지 못하는 변동성의 합으로, 모델의 전반적인 예측 성능을 평가하는 데 사용됩니다.
SST = ∑(i=1 to n) (yi - ȳ)^2
SST는 SSE와 SSR의 합과 같습니다. 즉, SST = SSE + SSR입니다. 이 관계식은 다음과 같이 증명할 수 있습니다.
SST = ∑(yi - ȳ)²
= ∑[(yi - ŷi) + (ŷi - ȳ)]²
= ∑(yi - ŷi)² + 2∑(yi - ŷi)(ŷi - ȳ) + ∑(ŷi - ȳ)²
= SSE + 2∑(yi - ŷi)(ŷi - ȳ) + SSR
= SSE + SSR (단, 2∑(yi - ŷi)(ŷi - ȳ)는 0이 됩니다.)
수식으로 설명지표 간 관계를 다시 정리하면 아래와 같습니다.
SST = SSR + SSE
R-Squared = SSR / SST = (SST – SSE) / SST = 1 – (SSE / SST)
MSE = SSE / (N - K - 1)
선형 회귀 모델 해석 방법
회귀 계수(Coefficients): 각 독립 변수의 회귀 계수는 해당 독립 변수가 종속 변수에 얼마나 영향을 미치는지를 나타냅니다. 회귀 계수가 양수일 경우, 독립 변수의 값이 증가할 때 종속 변수의 값도 증가합니다. 반대로, 회귀 계수가 음수일 경우, 독립 변수의 값이 증가할 때 종속 변수의 값은 감소합니다. 모델의 성능 평가는 주로 잔차(residual)를 계산하고, 잔차의 합이 최소가 되도록 모델을 조정하는 방법으로 이루어집니다. 이를 최소제곱법(least squares method)이라고 합니다.
R-squared: R-squared는 모델이 데이터를 얼마나 잘 설명하는지를 나타내는 지표입니다. R-squared는 0에서 1 사이의 값을 가지며, 1에 가까울수록 모델이 데이터를 잘 설명한다는 의미입니다. 하지만, R-squared가 높다고 해서 모델이 반드시 좋은 모델은 아닙니다.
F-검정(F-test): F-검정은 전체 모델이 유의한지 여부를 판단하는데 사용됩니다. F-검정에서 p-value가 낮을수록 모델이 데이터를 잘 설명하며, 유의미하다는 것을 의미합니다.
잔차(Residuals): 잔차는 실제 값과 모델이 예측한 값 간의 차이를 나타냅니다. 잔차가 작을수록 모델이 데이터를 잘 설명하고 있다는 의미입니다. 잔차를 시각적으로 확인하여 모델이 데이터를 얼마나 잘 설명하는지를 판단할 수도 있습니다.
가정(Assumptions): 선형 회귀 모델을 적용하기 위해서는 일정한 가정이 필요합니다. 이러한 가정은 독립 변수와 종속 변수 간의 선형적인 관계, 잔차의 정규성, 독립성, 등분산성 등이 있습니다. 이러한 가정들이 만족되지 않는 경우, 모델이 잘못된 결과를 도출할 수 있습니다.
따라서, 선형 회귀 모델을 해석할 때는 위와 같은 요소들을 종합적으로 고려하여 결과를 분석해야 합니다.

변수간 관계가 선형이 아닌 경우
선형 회귀 모델을 적용하기 위해서는 독립 변수와 종속 변수 간에 선형적인 관계가 존재해야 합니다. 만약 독립 변수와 종속 변수 간에 비선형적인 관계가 존재하는 경우, 선형 회귀 모델을 적용할 수 없습니다. 이 경우에는 다음과 같은 방법들을 고려해볼 수 있습니다.
비선형 모델 적용: 비선형 모델을 적용하여 독립 변수와 종속 변수 간의 관계를 모델링할 수 있습니다. 이러한 모델은 선형 회귀 모델보다 유연하며, 비선형적인 관계를 잘 모델링할 수 있습니다.
변수 변환: 독립 변수나 종속 변수를 로그, 제곱근 등의 함수를 이용하여 변환할 수 있습니다. 이를 통해 비선형적인 관계를 선형적인 관계로 변환할 수 있습니다.
상호작용 항 추가: 독립 변수들 간의 상호작용 항을 추가하여 비선형적인 관계를 모델링할 수 있습니다. 예를 들어, x1과 x2 간의 곱인 x1*x2 항을 추가할 수 있습니다.
다항 회귀(Polynomial Regression): 독립 변수의 차수를 늘려서 다항 회귀 모델을 적용할 수 있습니다. 이를 통해 비선형적인 관계를 모델링할 수 있습니다.
이러한 방법들을 고려하여 비선형적인 관계를 모델링할 수 있습니다. 하지만, 모델의 유효성을 확인하기 위해서는 모델의 예측력을 평가하는 것이 중요합니다. 따라서, 적절한 모델을 선택하고 평가하는 것이 필요합니다.
'확률통계 > 회귀분석' 카테고리의 다른 글
| 로지스틱 회귀(Logistic Regression) (0) | 2023.03.28 |
|---|---|
| 정규화 (Regularization) (0) | 2023.03.20 |
