정규화 (Regularization)

회귀분석에서 regularization은 모델이 과적합(overfitting)되지 않도록 하기 위해 모델의 복잡도를 제한하는 기법입니다. Regularization은 모델이 예측할 때 사용되는 변수의 개수를 줄이는 것으로, 모델의 복잡도를 줄여서 일반화 성능을 높이는 것을 목적으로 합니다. Regularization은 주로 선형 회귀 모델에서 사용됩니다. 일반적으로 선형 회귀 모델에서 가중치(w)의 크기가 큰 경우, 모델은 과적합될 가능성이 높아집니다. 따라서 regularization은 가중치의 크기를 제한하는 방법으로 모델의 과적합을 방지합니다.

선형 회귀 모델에서는 주로 L1 regularization(Lasso)과 L2 regularization(Ridge)이 사용됩니다. L1 regularization은 가중치의 절댓값 합을 최소화하는 것으로, 가중치를 0으로 만드는 효과가 있습니다. 이를 통해 불필요한 변수를 제거할 수 있습니다. L2 regularization은 가중치의 제곱 합을 최소화하는 것으로, 가중치를 작게 만들어 과적합을 방지하는 효과가 있습니다.

정규화를 소개하기 위해 난수를 생성하여 데이터 셋을 만들어 보았습니다.

 

L1 regularization (lasso)

 

Lasso라고도 불리며, 회귀 모델에서 사용되는 변수들의 계수를 0으로 만드는 기법입니다. 이를 통해 불필요한 변수를 제거하고 모델의 복잡도를 줄일 수 있습니다. L1 regularization은 가중치 벡터의 절대값 합을 최소화하는 것이 목적입니다.

L1 regularization을 수식으로 나타내면 다음과 같습니다.
L1 regularization = α ∑|w|

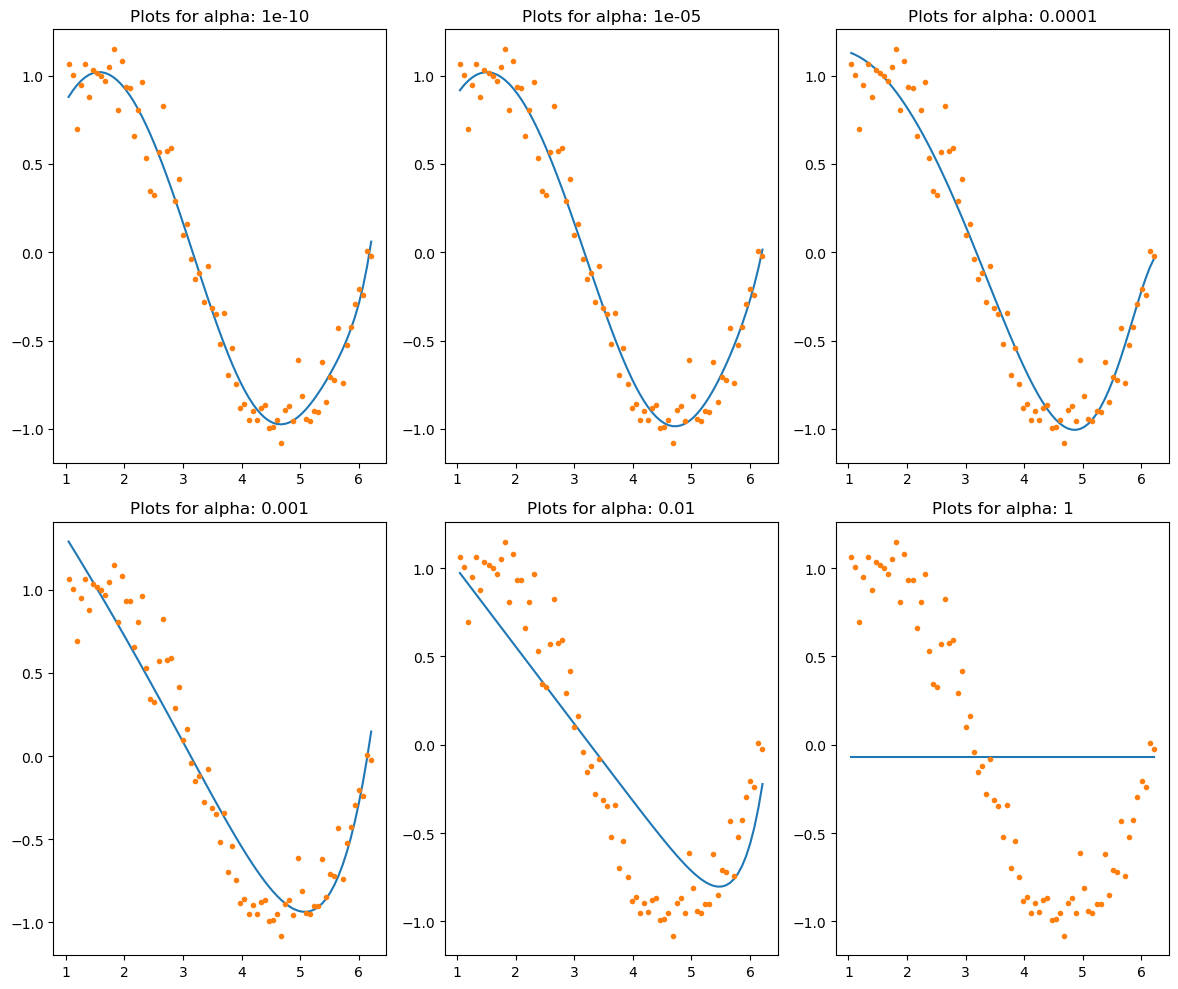
여기서 α는 regularization 강도를 조절하는 하이퍼파라미터입니다. α가 0이면 regularization이 없는 일반적인 선형 회귀와 같아집니다. α가 커질수록 regularization 강도가 강해져서 가중치의 크기를 작게 만듭니다. L1 regularization을 사용하면 가중치 벡터의 일부 원소들은 0으로 수렴할 가능성이 높아집니다. 이는 모델에서 해당 변수를 제외시키는 역할을 합니다. 따라서 L1 regularization은 feature selection에 사용될 수 있습니다.

L1 regularization은 변수가 많은 모델에서 특히 유용합니다. 변수가 많은 경우에는 가중치 벡터의 일부 원소들이 너무 큰 값을 가질 수 있습니다. 이런 경우에는 L1 regularization을 사용하여 가중치 벡터의 크기를 작게 만들 수 있습니다. 

 

α 가중치 값에 따른 결과: lasso

 

 

 

L2 regularization (ridge)

 

Ridge regression이라고도 불리며, 회귀 모델에서 사용되는 변수들의 계수를 줄이는 기법입니다. 이를 통해 모델의 과적합을 방지하고 일반화 성능을 향상시킬 수 있습니다. L2 regularization은 가중치 벡터의 제곱합을 최소화하는 것이 목적입니다.

L2 regularization을 수식으로 나타내면 다음과 같습니다.
L2 regularization = α ∑w^2

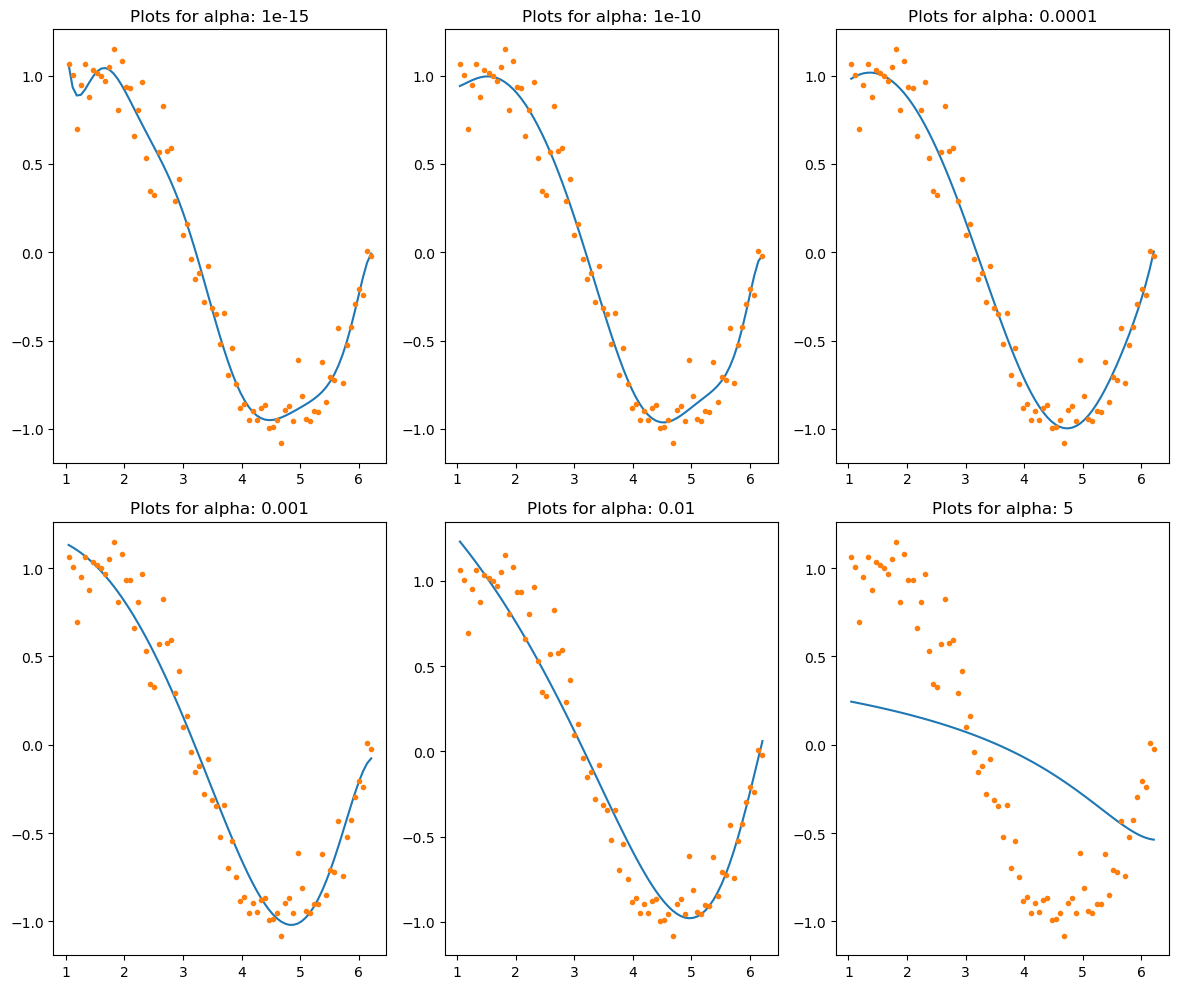
Ridge regression에서는 하이퍼파라미터인 α를 사용하여 regularization 강도를 조절합니다. α가 크면 regularization 강도가 강해져서 가중치 값들이 더 작아지게 됩니다. α가 작으면 regularization 강도가 약해져서 가중치 값들이 더 커지게 됩니다.

Ridge regression에서 α가 0이면 일반적인 선형 회귀와 같아지게 됩니다. 즉, regularization이 없는 경우입니다. 따라서 모델에서 가중치 값들이 자유롭게 조절될 수 있습니다. 그러나 α가 커질수록 regularization 강도가 강해져서 가중치 값들이 작아지게 됩니다. 이는 모델에서 각 변수의 영향력을 낮추는 역할을 합니다.

따라서 Ridge regression에서는 하이퍼파라미터인 α의 값이 가중치 값들에 어떤 영향을 미치는지를 조절할 수 있습니다. 적절한 α값을 선택하면 Ridge regression 모델에서 좋은 예측 성능을 얻을 수 있습니다. 그러나 α값이 너무 크면 모델이 과소적합되어 성능이 저하될 수 있으며, α값이 너무 작으면 모델이 과적합되어 성능이 저하될 수 있습니다. 따라서 α값을 조정하면서 적절한 값으로 설정하는 것이 중요합니다.

 

α 가중치 값에 따른 결과: ridge

 

 

Lasso와 Ridge의 공통점과 차이점

공통점:

• 모두 회귀 모델에서 가중치 값을 제한하기 위한 Regularization 방법입니다
• Regularization을 통해 모델의 과적합을 방지하고 일반화 성능을 향상시킬 수 있습니다
• 둘 다 하이퍼파라미터인 α를 사용하여 regularization 강도를 조절합니다.

 

차이점:

• Lasso는 L1 regularization을 사용하여 가중치 값들을 0으로 만들 수 있습니다. 즉, Lasso는 변수 선택 기능을 수행할 수 있습니다. 이는 변수 간 상호작용이 적을 때 유용합니다.
• Ridge는 L2 regularization을 사용하여 가중치 값을 작게 만듭니다. Ridge는 Lasso와 달리 변수 선택 기능을 수행하지 않습니다.
• Lasso는 약간의 가중치 값을 가진 변수들이 많고, 나머지 변수들은 0에 가까운 가중치 값을 가지게 됩니다. 이는 특정 변수들이 예측에 중요한 역할을 하는 경우 유용합니다.
• Ridge는 모든 변수들이 약간의 가중치 값을 가지게 됩니다. 이는 특정 변수들이 예측에 미치는 영향이 크게 다르지 않은 경우 유용합니다.

 

Lasso와 Ridge는 모두 Regularization을 통해 모델의 과적합을 방지하고 일반화 성능을 향상시키는 목적을 가지고 있습니다. Lasso는 변수 선택 기능을 수행하여 특정 변수들의 중요도를 파악하는데 유용하며, Ridge는 모든 변수들을 적절하게 조절하는데 유용합니다.