[데이터_공예소]

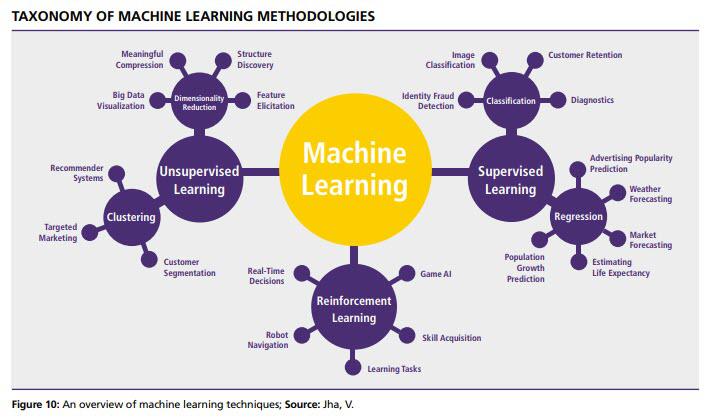
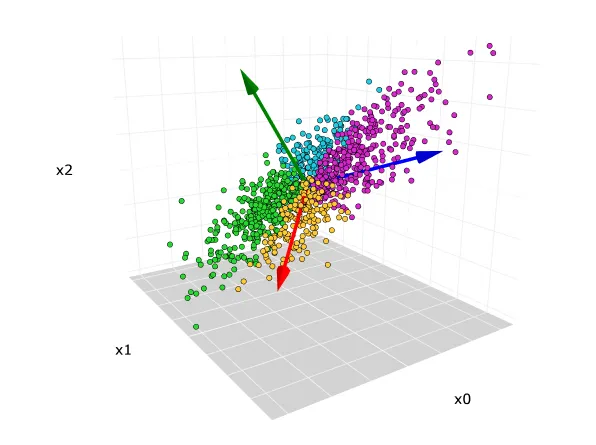
머신러닝의 흐름을 이해할 수 있도록 분류체계에 대한 이해를 돕고자 한다. 서플라이체인과 관련하여 머신러닝이 사용된다는 포브스의 기사가 있고 관련 사진을 공유한다. 시간이 되시는 분들은 출처링크에 가서 기사를 읽어보는 것을 추천한다. Forbes - 10 Ways Machine Learning Is Revolutionizing Supply Chain Management 머신러닝의 3가지 분류 지도학습(Supervised Learning) - 분류 , 회귀 정답을 알려주며 학습시키는 것을 의미한다. 환자별 질병 증상데이터에(input) 발병 미발병 등 (labelling)을 기록하여 컴퓨터에 전달한다. 컴퓨터는 학습과 검증데이터를 통해(train set, test set) 학습이 올바로 되었는지 확인할 수 ..

기계가 데이터를 사람처럼 학습하고 인사이트를 도출해 내는 과정이다 보니, 선형대수, 통계, 회귀분석 등 다양한 분야에서 많은 토픽이 등장한다. 주요 용어를 간단히 정리해 보았는데 용어를 보면서 이 용어에 대해 어느정도 이해도가 있는지 스스로 진단하고 부족한 부분에 대해서는 추가적인 학습을 하고 이해도를 높여나가는 방식으로 공부를 진행할 수 있을 것이다. 인공지능 (Artificial Intelligence): 컴퓨터 프로그램이 인간의 학습 능력, 추론 능력, 언어 이해 능력, 시각 및 청각 인식 능력 등 인간의 지적 능력을 모방하는 기술. 기계 학습 (Machine Learning): 컴퓨터가 데이터를 분석하고 패턴을 인식하여 스스로 학습하고 결정을 내릴 수 있는 능력을 갖춘 기술. 딥 러닝 (Deep ..

주성분 분석(Principal Component Analysis, PCA)은 머신러닝에서 차원 축소에 사용되는 비지도학습 알고리즘입니다. 상관관계가 있는 여러 특성들의 관측치를 직교 변환을 통해 선형적으로 상관성이 없는 주성분으로 변환하고 이러한 변환된 새로운 특성들은 주성분이라고 부릅니다. 주성분 분석은 탐색적 데이터 분석과 예측 모델링에 많이 사용되며 데이터셋의 분산을 줄이기 위해 강력한 패턴을 도출하는 방법입니다. 아래와 같은 3차원 데이터 셋을 가정하는 겁니다. 3개의 축을 기준으로 각 데이터의 위치를 설명해야 합니다. PCA는 일반적으로 고차원 데이터를 투영할 저차원 면을 찾는데, 이는 각 특성의 분산을 고려하여 작동합니다. 분산이 높을수록 좋은 분류가 가능하므로 데이터 차원을 축소시킵니다. P..

ML/AI 를 공부할 때 등장하는 확률 통계 용어를 정리하고자 합니다. ML/AI에서 이를 다루는 이유는 확률은 불확실성을 표현하는 언어 라고 보시면 됩니다. 머신러닝, 인공지능분야는 확률의 관점에서 결론을 내리기 때문입니다. 사진학습 예시: [p(lion), p(tiger)] = [0.01, 0.99] [p(lion), p(tiger)] = [0.98, 0.02] 향후 관심을 가지고 현업에 계시거나 혹은, 논문을 보실 때 나올만한 용어를 정리합니다. 확률론 (probability theory) : 실제로 발생하는 다양한 결과들의 기회 혹은 가능성을 이해하거나 설명하는 이론. 표본공간과 사건 (Sample space, Event) 표본공간(sample space) : 실험에 의하여 가능한 모든 결과의 집..

학교에 가던, 인강을 틀고 딥러닝 수업을 보면 항상 딥러닝 외에 배경 이야기가 정말 많습니다. 통계, 최적화, 파이썬 패키지 사용법부터 시작해서 딥러닝을 직접 다루기 전까지 기초설명이 많은데요, 그래서 딥러닝을 배우려고 하면 정말, 솔직히 정신이 산만해진다는 생각이 듭니다. 딥러닝은 기계 학습의 한 분야로, 입력 데이터와 출력 데이터 사이의 복잡한 관계를 모델링하기 위해 인공 신경망을 사용합니다. 이 과정에서 미분이 매우 중요한 역할을 합니다. 미분은 함수의 변화율을 나타내며, 딥러닝에서는 이를 통해 손실 함수(loss function)의 기울기(gradient)를 계산합니다. 이 기울기는 모델의 가중치(weight)를 업데이트하는 데 사용됩니다. 즉, 기울기가 큰 방향으로 가중치를 업데이트하여 손실 함..